Рисунки графиков функций, Рисунки из графиков функций. Ландыш Колокольчик «Ландыш» 1) - презентация

Для этого после изучения следующей таблицы рекомендую пройти по ссылке "Преобразования графиков функций". Принципиально такой же вид имеют графики функций-многочленов 5-й, 7-й, 9-й и других нечетных степеней. Итак, как нам нарисовать график производной? Степенная функция Задания для устного счета Упражнение 6 10 класс. С помощью графических рисунков и диаграмм студенты могут наглядно увидеть, как меняются значения функций в зависимости от различных параметров.
Разберем принципы позволяющие оптимизировать процедуру построения графиков, узнаем как строить графики разрывных функций. Также узнаем, что такое метод наименьших квадратов и многочлен Лагранжа.
Немного на заметку. Рисуем по координатам. Математика для всех. Здравствуйте, уважаемые читатели! В статье о декартовой системе координат я писал о том, что в будущем можно будет подробнее разобрать понятия "функция" и "график функции". Сегодня я как раз хочу поговорить на эту тему. На самом деле эта тема настолько обширна, что не поместится даже в самой большой библиотеке, если рассматривать всё возможное многообразие функций. Их просто бесконечное количество. Это как попытаться найти и записать самое большое простое число или что-то в этом роде.
Для решения задачи нужно обладать навыками:. Канал в Telegram. Канал в Дзен. Группа в ВК. Универ на диване. Немного об инженерной графике. Здравствуйте, Дорогие друзья! Сегодня мы с Вами поговорим о геометрии и инженерной графике. Первым делом вспомним трехмерную Декартову систему координат.
Кому это словосочетание ни о чём не говорит, поясняю: оси X, Y, Z. Каждые две оси лежат в одной плоскости. Название плоскостей состоит обычно из названий осей: Для тех, кто только-только начал знакомиться с 3Д поясняю простой принцип: на плоскости строится фигура, в пространстве а именно пространство образуется из трёх плоскостей строятся поверхности и модели Задача с кодом. Расстояние между точками. Напишите функцию, которая будет принимать координаты двух точек в двумерной декартовой системе координат и возвращать расстояние между этими точками.
Координаты будут передаваться в функцию в виде строки из четырех чисел через запятую:. Примечание: если расстояние окажется числом с плавающей запятой, его нужно округлить до сотых например, 2. Решение на нашем сайте. Репетитор IT mentor. О полярных координатах и нахождении площади в полярной системе координат. Полярная система координат на плоскости — координаты объекта, выраженные через направление и расстояние. Эта система включает в себя точку отсчета — полюс и луч , начинающийся в этой точке, — полярную ось На бумаге экономят.
Для оформления контрольных работ рекомендую использовать тетради Архангельского ЦБК 18 листов, клетка или «Пятёрочку», правда, она дороже. Ручку желательно выбрать гелевую, даже самый дешевый китайский гелевый стержень намного лучше, чем шариковая ручка, которая то мажет, то дерёт бумагу. Единственной «конкурентоспособной» шариковой ручкой на моей памяти является «Эрих Краузе».
Она пишет чётко, красиво и стабильно — что с полным стержнем, что с практически пустым. Дополнительно : вИдение прямоугольной системы координат глазами аналитической геометрии освещается в статье Линейная не зависимость векторов.
Базис векторов , подробную информацию о координатных четвертях можно найти во втором параграфе урока Линейные неравенства. Стандарт: ось аппликат — направлена вверх, ось — направлена вправо, ось — влево вниз строго под углом 45 градусов.
Масштаб по оси — меньше, чем масштаб по другим осям. Также обратите внимание, что на правом чертеже я использовал нестандартную «засечку» по оси о такой возможности уже упомянуто выше. С моей точки зрения, так точнее, быстрее и эстетичнее — не нужно под микроскопом выискивать середину клетки и «лепить» единицу впритык к началу координат. Для чего нужны все эти правила?
Правила существуют для того, чтобы их нарушать. Чем я сейчас и займусь. Дело в том, что последующие чертежи статьи будут выполнены мной в Экселе, и, координатные оси будут выглядеть некорректно с точки зрения правильного оформления.
Я бы мог начертить все графики от руки, но чертить их на самом деле жуть как неохота Эксель их начертит гораздо точнее. Линейная функция задается уравнением. График линейной функций представляет собой прямую. Для того, чтобы построить прямую достаточно знать две точки. Построить график функции. Найдем две точки. В качестве одной из точек выгодно выбрать ноль. Если , то. А сами значения рассчитываются устно или на черновике, калькуляторе.
При оформлении чертежа всегда подписываем графики. Обратите внимание, как я расположил подписи, подписи не должны допускать разночтений при изучении чертежа.
В данном случае крайне нежелательно было поставить подпись рядом с точкой пересечения прямых , или справа внизу между графиками. График прямой пропорциональности всегда проходит через начало координат. Таким образом, построение прямой упрощается — достаточно найти всего одну точку.
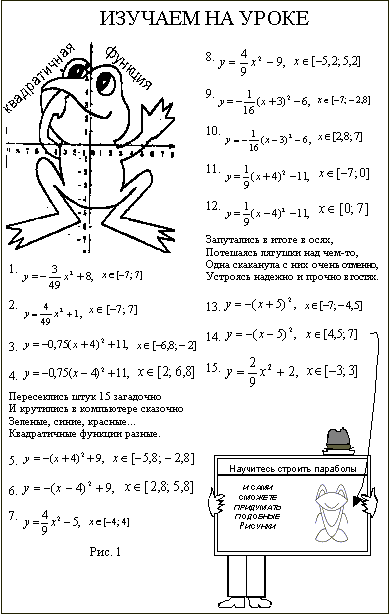
График функции строится сразу, без нахождения всяких точек. То есть, запись следует понимать так: «игрек всегда равен —4, при любом значении икс». График функции также строится сразу. Запись следует понимать так: «икс всегда, при любом значении игрек, равен 1». Некоторые спросят, ну зачем вспоминать 6 класс?! Так-то оно, может и так, только за годы практики я встретил добрый десяток студентов, которых ставила в тупик задача построения графика вроде или.
Прямая линия детально рассматривается в курсе аналитической геометрии, и желающие могут обратиться к статье Уравнение прямой на плоскости. График квадратичной функции представляет собой параболу. Рассмотрим знаменитый случай:. Вспоминаем некоторые свойства функции. Область определения — любое действительное число любое значение «икс».
Что это значит? Какую бы точку на оси мы не выбрали — для каждого «икс» существует точка параболы. Математически это записывается так:. Область определения любой функции стандартно обозначается через или. Буква обозначает множество действительных чисел или, проще говоря, «любое икс» когда работа оформляется в тетради, пишут не фигурную букву , а жирную букву R. Область значений — это множество всех значений, которые может принимать переменная «игрек». В данном случае: — множество всех положительных значений, включая ноль.
Область значений стандартно обозначается через или. Функция является чётной. Если функция является чётной, то ее график симметричен относительно оси. Это очень полезное свойство, которое заметно упрощает построение графика, в чём мы скоро убедимся. Аналитически чётность функции выражается условием. Как проверить любую функцию на чётность?
Нужно вместо подставить в уравнение. В случае с параболой проверка выглядит так: , значит, функция является четной. Функция не ограничена сверху. Аналитически свойство записывается так:. Вот вам, кстати, и пример геометрического смысла предела функции: если мы будем уходить по оси влево или вправо на бесконечность, то ветки параболы значения «игрек» будут неограниченно уходить вверх на «плюс бесконечность».
При изучении пределов функций желательно понимать геометрический смысл предела. Я не случайно так подробно расписал свойства функции, все вышеперечисленные вещи полезно знать и помнить при построении графиков функций, а также при исследовании графиков функций. В этом примере мы рассмотрим важный технический вопрос: Как быстро построить параболу?
В практических заданиях необходимость начертить параболу возникает очень часто, в частности, при вычислении площади фигуры с помощью определенного интеграла. Поэтому чертеж желательно научиться выполнять быстро, с минимальной потерей времени.
Я предлагаю следующий алгоритм построения. Если с производными плохо, следует ознакомиться с уроком Как найти производную? Итак, решение нашего уравнения: — именно в этой точке и находится вершина параболы.
Почему это так, можно узнать из теоретической статьи о производной и урока об экстремумах функции. А пока рассчитываем соответствующее значение «игрек»:. Таким образом, вершина находится в точке.
Теперь находим другие точки, при этом нагло пользуемся симметричностью параболы. Следует заметить, что функция — не является чётной , но, тем не менее, симметричность параболы никто не отменял. Данный алгоритм построения образно можно назвать «челноком» или принципом «туда-сюда» с Анфисой Чеховой. Из рассмотренных графиков вспоминается еще один полезный признак:.
Для квадратичной функции справедливо следующее:. Если , то ветви параболы направлены вверх. Если , то ветви параболы направлены вниз. Углублённые знания о кривой можно получить на уроке Гипербола и парабола. Кубическая парабола задается функцией.
Вот знакомый со школы чертеж:. Перечислим основные свойства функции. Область определения — любое действительное число:. Область значений — любое действительное число:. Функция является нечётной. Если функция является нечётной, то ее график симметричен относительно начала координат.
Аналитически нечётность функции выражается условием. Выполним проверку для кубической функции, для этого вместо «икс» подставим «минус икс»: , значит, функция является нечетной.
Функция не ограничена. На языке пределов функции это можно записать так: ,. Наверняка, вы заметили, в чем ещё проявляется нечетность функции. Если мы нашли, что , то при вычислении уже не нужно ничего считать, автоматом записываем, что.
Эта особенность справедлива для любой нечетной функции. А теперь поговорим о графиках функций-многочленов высоких степеней чуть более подробно. График функции принципиально имеет следующий вид:. В этом примере коэффициент при старшей степени , поэтому график развёрнут «наоборот».
Принципиально такой же вид имеют графики функций-многочленов 5-й, 7-й, 9-й и других нечетных степеней. Чем выше степень, тем больше промежуточных «загибулин». Функции-многочлены 4-й, 6-й и других четных степеней имеют график принципиально следующего вида:.
Эти знания полезны при исследовании графиков функций. Он представляет собой одну из ветвей параболы. Выполним чертеж:. Основные свойства функции :. Область определения :. Область значений:. Или с помощью предела:. При построении простейших графиков с корнями также уместен поточечный способ построения, при этом выгодно подбирать такие значения «икс», чтобы корень извлекался нацело:. На самом деле хочется разобрать еще примеры с корнями, например, , но они встречаются значительно реже.
Сейчас я ориентируюсь на более распространенные случаи, и, как показывает практика, что-нибудь вроде приходиться строить значительно чаще.
Однако унывать не нужно, в других статьях я рассмотрю самые разнообразные функции и их графики, корни в том числе. Опять же вспоминаем тривиальную «школьную» гиперболу. Выполним чертеж: Основные свойства функции :. Запись обозначает: «любое действительное число, исключая ноль». В точке функция терпит бесконечный разрыв. Или с помощью односторонних пределов: ,. Немного поговорим об односторонних пределах. Запись обозначает, что мы бесконечно близко приближаемся по оси к нулю слева.
Как при этом ведёт себя график? Он уходит вниз на минус бесконечность, бесконечно близко приближаясь к оси. Именно этот факт и записывается пределом. Аналогично, запись обозначает, что мы бесконечно близко приближаемся по оси к нулю справа.
При этом ветвь гиперболы уходит вверх на плюс бесконечность, бесконечно близко приближаясь к оси. Или коротко:. Такая прямая к которой бесконечно близко приближается график какой-либо функции называется асимптотой.
В данном случае ось является вертикальной асимптотой для графика гиперболы при. Также односторонние пределы , говорят нам о том, что гипербола не ограничена сверху и не ограничена снизу. Исследуем функцию на бесконечности: , то есть, если мы начнем уходить по оси влево или вправо на бесконечность, то «игреки» стройным шагом будут бесконечно близко приближаться к нулю, и, соответственно, ветви гиперболы бесконечно близко приближаться к оси.
Таким образом, ось является горизонтальной асимптотой для графика функции , если «икс» стремится к плюс или минус бесконечности. Функция является нечётной , а, значит, гипербола симметрична относительно начала координат. Данный факт очевиден из чертежа, кроме того, легко проверяется аналитически:. График функции вида представляет собой две ветви гиперболы. Если , то гипербола расположена в первой и третьей координатных четвертях см. Если , то гипербола расположена во второй и четвертой координатных четвертях.
Указанную закономерность места жительства гиперболы нетрудно проанализировать с точки зрения геометрических преобразований графиков. Построить правую ветвь гиперболы.
Используем поточечный метод построения, при этом, значения выгодно подбирать так, чтобы делилось нацело:. Не составит труда построить и левую ветвь гиперболы, здесь как раз поможет нечетность функции. Грубо говоря, в таблице поточечного построения мысленно добавляем к каждому числу минус, ставим соответствующие точки и прочерчиваем вторую ветвь.
Детальную геометрическую информацию о рассмотренной линии можно найти в статье Гипербола и парабола. Напоминаю, что — это иррациональное число: , это потребуется при построении графика, который, собственно, я без церемоний и построю. Трёх точек, пожалуй, хватит:. График функции пока оставим в покое, о нём позже. Область определения : — любое «икс». Обратите внимание, что ноль не включается в область значений.
Экспонента — функция положительная , то есть для любого «икс» справедливо неравенство , а сам график экспоненты полностью расположен в верхней полуплоскости.
Функция не ограничена сверху: , то есть, если мы начнем уходить по оси вправо на плюс бесконечность, то соответствующие значения «игрек» стройным шагом будут тоже уходить вверх на по оси. Кстати, график экспоненциальной функции будет «взмывать» вверх на бесконечность очень быстро и круто, уже при. Исследуем поведение функции на минус бесконечности:. Таким образом, ось является горизонтальной асимптотой для графика функции , если Принципиально такой же вид имеет любая показательная функция , если.
Функции , , будут отличаться только крутизной наклона графика, причем, чем больше основание, тем круче будет график. Обратите внимание, что во всех случаях графики проходят через точку , то есть. Это значение должен знать даже «двоечник». Теперь рассмотрим случай, когда основание. Снова пример с экспонентой — на чертеже соответствующий график прочерчен малиновым цветом? Что произошло? Ничего особенного — та же самая экспонента, только она «развернулась в другую сторону».
Об этой метаморфозе можно получить подробную информацию в статье Построение графиков с помощью геометрических преобразований. Принципиально так же выглядят графики функций , и т. Должен сказать, что второй случай встречается на практике реже, но он встречается, поэтому я счел нужным включить его в данную статью.
Рассмотрим функцию с натуральным логарифмом. Выполним поточечный чертеж:. Функция не ограничена сверху: , пусть и медленно, но ветка логарифма уходит вверх на бесконечность. Исследуем поведение функции вблизи нуля справа:. Таким образом, ось является вертикальной асимптотой для графика функции при «икс» стремящемся к нулю справа. Обязательно нужно знать и помнить типовое значение логарифма :.
Принципиально так же выглядит график логарифма при основании : , , десятичный логарифм по основанию 10 и т. При этом, чем больше основание, тем более пологим будет график. Случай рассматривать не будем, что-то я не припомню, когда последний раз строил график с таким основанием. Да и логарифм вроде в задачах высшей математики ооочень редкий гость. В заключение параграфа скажу еще об одном факте: Экспоненциальная функция и логарифмическая функция — это две взаимно обратные функции.
Если присмотреться к графику логарифма, то можно увидеть, что это — та же самая экспонента, просто она расположена немного по-другому. Построим график функции.
Напоминаю, что «пи» — это иррациональное число: , и в тригонометрии от него в глазах рябит. Данная функция является периодической с периодом. Посмотрим на отрезок. Слева и справа от него бесконечно повторяется точно такой же кусок графика.