Скорость и ускорение материальной точки, Скорость материальной точки.

Оно имеет две компоненты: радиальное и касательное. Тангенциальное и нормальное ускорение. Типичным примером неравномерного движения является свободное падение тел. Ускорение свободного падения Собственное ускорение Релятивистски равноускоренное движение Приливное ускорение Кориолисово ускорение Рывок кинематика.
Логин: Пароль: Забыли пароль? Email: Email повторно: Логин: Пароль: Принимаю пользовательское соглашение. FAQ Обратная связь Вопросы и предложения.
Добавил: Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам. Скачиваний: Силы тяготения гравитационные силы.

Силы упругости. Сила трения скольжения. Потенциальная энергия. Общефизический закон сохранения. Уравнение вращательного движения твердого тела относительно точки. Теорема Штейнера. Принцип относительности в механике.
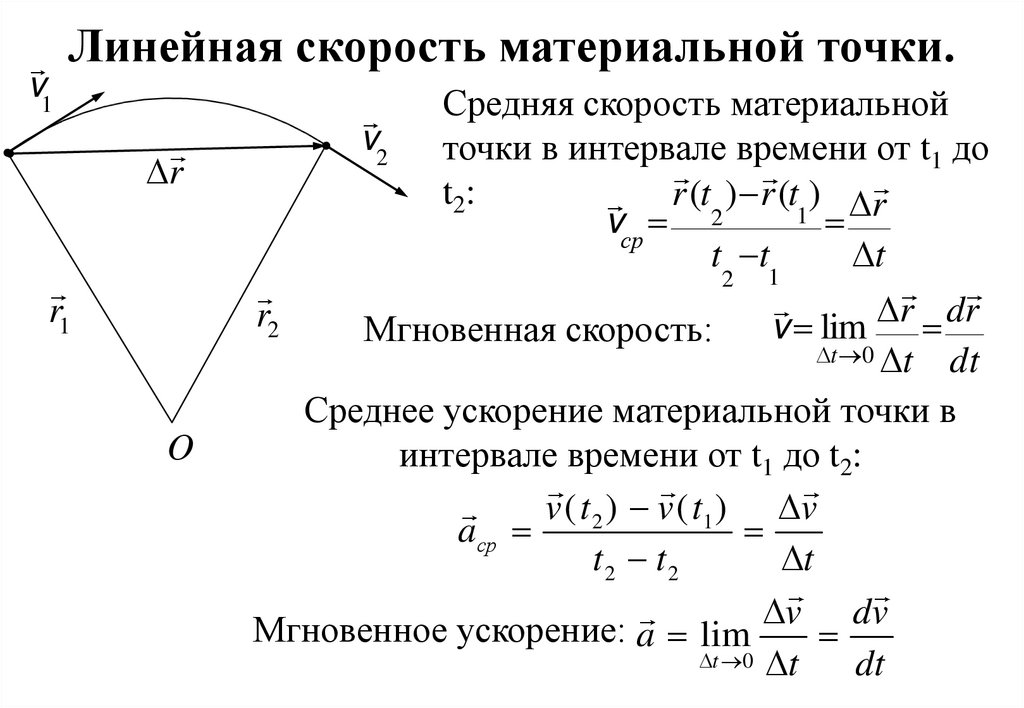
Скорость материальной точки. Средней векторной скоростью материальной точки называют отношение приращения радиус-вектора точки к тому промежутку времени, за которые это приращение произошло: 1 Средняя путевая скорость: В Международной системе СИ единицей расстояния является метр, единицей времени — секунда, поэтому скорость выражается в метрах в секунду: Если , то отношение стремится к некоторому пределу, называемому скоростью материальной точки в момент времени t или мгновенной скоростью : 2 Мгновенной скоростью точки называют вектор, численно равный первой производной по времени от радиус-вектора, определяющего положение этой точки в данный момент времени.
Если при движении тела его скорость изменяется по модулю и или направлению, то можно ввести понятие ускорения. Ускорение есть векторная физическая величина, определяемая как отношение малого изменения скорости к малому промежутку времени за который произошло это изменение:. Коэффициент пропорциональности a — ускорение тела.
При равноускоренном движении ускорение тела постоянно. В общем случае ускорение тела — векторная величина. При движении тела вдоль прямой линии ускорение можно определить по формуле: где — изменение скорости тела за время t.
В этом случае ускорение описывается скалярной величиной.

Выражение для перемещения s может быть представлено в виде:. В Занятиях 8 и 9 дан физический смысл тангенциального и нормального ускорений.
В Занятиях 10 и 11 рассмотрен частный случай криволинейного движения движение материальной точки по окружности. Занятие 6 посвящено рассмотрению физического смысла производной и её нахождению.
Условие задачи. Материальная точка двигается по окружности радиусом 4 м согласно следующему уравнению зависимости пути от времени:.

Взяв производную от пути по времени, получим уравнение зависимости её скорости от времени:. Выражение зависимости тангенциальной составляющей ускорения от времени получим, взяв производную от скорости по времени:. Нормальную составляющую ускорения находим по формуле:. Вектора тангенциального и нормального ускорений направлены друг к другу под прямым углом.