Основы кубика рубика, Математика кубика Рубика — Википедия

Скоростной метод CLL. Спасибо всё понятно, всё просто, очень помогли ,спасибо за схемы и видео. Расставляем ребра и углы по местам. Нижний крест и нижние угловые кубики собираются довольно просто, но если есть затруднения, то не так сложно приспособить Y-движение для этого или посмотреть одну из инструкций для простой послойной сборки кубика. Архивировано 9 января года.
Обратим внимание, что если повернуть грань кубика, то мы поменяем местами одновременно четыре рёберных кубика, что будет эквивалентно трём перестановкам, то есть нечётному числу, что нам и нужно. Из этого следует, что верхняя грань должна быть правильно ориентирована для того, чтобы мы могли собрать последние три рёберных кубика. Если так вышло, что последние три рёберных кубика требуют одной перестановки, то это значит, что нужно переставить на соседние места два рёберных кубика, уже собранные на верхней грани.
Кроме того, мы можем заранее, до сборки первых двух кубиков из этой пятёрки, подсчитать число перестановок, которые потребуются, чтобы поставить все пять рёберных кубиков на свои места. Если это число чётное, то верхняя грань ориентирована правильно.
А если нечётное, то её нужно повернуть один раз в любую сторону. Таким образом, мы сразу сможем поставить те два кубика на нужные места. Работа с угловыми кубиками На последнем этапе сборки нам нужно переставлять угловые кубики местами и поворачивать их.
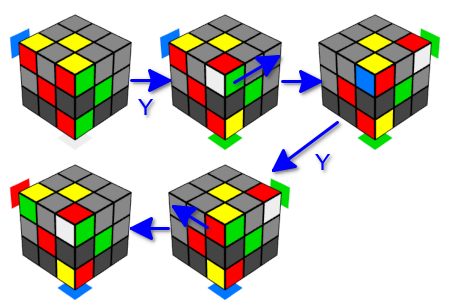
Для этого воспользуемся перечисленными ранее свойствами Y-движения в отношении угловых кубиков. В этом разделе будет использоваться именно эти варианты, без дополнительного уточнения. Обратим сразу внимание, что это движение меняет состояние только одного кубика на верхней грани — это угловой кубик на «смежном ребре».
Для перестановки угловых кубиков заметим, что одиночное Y-движение как левое, так и правое меняет местами пару угловых кубиков на «смежном ребре», а также что последовательное применение левого и правого Y-движения или правого и левого возвращает весь кубик в исходное состояние.
Давайте подумаем, что произойдёт, если между этими движениями мы повернём верхнюю грань. Как мы уже обратили внимание, на верхней грани меняется только один угловой кубик, который переставляется с парным кубиком на ребре. В таком случае у нас произойдёт два обмена угловыми кубиками на ребре, но каждый раз сверху будет подставлен разный угол, а все остальные кубики останутся как были конечно, нужно ещё не забыть повернуть верхнюю грань в исходное состояние.
Таким образом, мы осуществили обмен местами трёх угловых кубиков — одного с нижней грани и двух с верхней. Теперь разберёмся с поворотом кубиков. Для этого воспользуемся похожим трюком. Будем делать два последовательных Y-движения в одном направлении. В результате этого угловые кубики остаются на месте, но меняют свою ориентацию.
Тут нас интересуют два варианта комбинации движений: три двойных движения в одном направлении левые или правые или двойное движение в одном направлении и двойное движение в обратном направлении. В каждом из этих вариантов весь кубик возвращается в исходное состояние. И мы опять будем между двойными движениями подставлять очередной нужный нам угол на место верхнего угла «смежного ребра».
Таким образом мы можем повернуть либо три угловых кубика на одной грани в одном направлении, либо два угловых кубика на одной грани в разных направлениях, не меняя состояния остальных кубиков. Обратим внимание, что после двойного движения верхний кубик смежного ребра поворачивается в том же направлении, в котором осуществляется первое Y-движение. Заключение Не знаю как будет в вашем случае, но для меня плюс данного алгоритма не только в том, что его легко запомнить и не нужно зубрить инструкцию по сборке.

Но также и в том, что теперь, собирая кубик, я собираю его сам, понимая что происходит, вместо почти механического следования инструкции, а это намного приятнее. Чего и вам желаю! Теги: кубик рубика головоломки сделай сам. Хабы: Мозг Логические игры. Если эта публикация вас вдохновила и вы хотите поддержать автора — не стесняйтесь нажать на кнопку. Комментарии Отправить сообщение.
Комментарии Комментарии Лучшие за сутки Похожие. Серия занятий «Тренировки по алгоритмам 5. Оставить заявку. Курс «Кубик Рубика». Ваш ребенок давно мечтал «взломать» цветовые алгоритмы кубика Рубика? Тогда этот курс как раз то, что ему нужно. Мы покажем два разных способа сборки — тренируйтесь, развивайтесь и ставьте рекорды!
Для чего ребенку уметь собирать кубик Рубика? Кубик Рубика — настоящий тренажер для мозга! Ведь он развивает способности, связанные с пространством, логикой, мышлением и моторикой. Память и логика. Существуют алгоритмы сборки, которые нужно запомнить, а также понимать взаимосвязь действий и последствий. Сам процесс сборки тренирует быстрый анализ ситуации и принятие решений. Внимание и концентрация. В некоторых моделях есть пружинка, надетая на тонкий конец креста, позволяющая оттягивать при повороте поворачиваемый слой кубиков.
В центральных и бортовых кубиках с внутренней стороны сделаны вырезки таким образом, что получается полость в виде объединения трёх цилиндров. Кроме этого, на бортовых и угловых кубиках имеются выпуклости разной формы. Они образуют фрагмент цилиндра, который плотно входит в упомянутую выше полость. С помощью такой конструкции грани кубика свободно вращаются с внутренних сторон центральные, бортовые и угловые кубики имеют различные вырезы.
В таком кубике внутренний механизм выполнен не в виде креста, а в виде шара. Кубик крутится более плавно, мягче и при этом точнее. Благодаря новому механизму, теперь кубик Рубика «режет углы». Это означает, что даже если в процессе сборки какая-то из сторон кубика оказалась, не повернута до конца, то поворот другой стороны, пересекающей эту, довернет сторону. Это обновленный механизм на базе шара, с использованием пружинок и винтиков пользуется особой популярностью у спидкуберов — людей, соревнующихся в сборке кубика Рубика на скорость.
Сам кубик делается из более дорогой пластмассы.
Используется для профессиональной сборки и, к сожалению, у него высокая ценовая категория. Если вы решительны, вы их решите». Эрне Рубик.
Какой грандиозный успех сопровождает головоломку кубик Рубика с самого первого дня её изобретения! Различные механические головоломки по типу кубика Рубика создаются и в наше время. Очень велика польза механических головоломок для детей разного возраста. Моделирование из кубиков одноцветных дорожек разной длины, выстраивание сериационных рядов из 2 и 3 дорожек, отличающихся по длине. Другой частный случай классификации множества единичных кубиков , на которые разбит прямоугольный параллелепипед.
К данной задаче, в системе GeoGebra можно создать 3D-модель, причём, если использовать 3D-модель только в качестве наглядного пособия, то точное численное соблюдение всех значений величин пирамиды не требуется и достаточно просто с помощью средств данной программы В статье проведён анализ поведения кривой эффекта Даннинга-Крюгера и в результате обработки получена пара взаимосвязанных уравнений, описывающих поведение уровня самооценки в зависимости от уровня квалификации на этапах обучения и набора опыта.
Вершиной таких систем являются роботизированные предприятия, основа которых — промышленные манипуляторы. Манипулятор — механизм для управления пространственным положением орудий, объектов труда и конструкционных узлов и элементов. В статье рассматриваются учебные компьютерные программы как один из распространенных видов учебных моделей.
В качестве примера приводятся программы, моделирующие движение маятников. В статье описана компьютерная программа, моделирующая движение кругового математического маятника.
Кратко изложена методика применения этой программы для изучения механических колебаний в курсе физики. Краевский определяет модель как « систему элементов, воспроизводящую определенные стороны. Поэтому модель определяется обычно как некий объект система , исследование которого служит средством для. Нажимая кнопку «Отправить», вы даете согласие на обработку своих персональных данных.
Опубликовать статью в журнале. Механика кубика Рубика. Скачать электронную версию.